東洋大学 理工学部生体医工学科 教授
博士(理学)。専門分野は、整数論、代数学、ゼータ関数。日本数理生物学会、アメリカ数学会、日本数学会に所属し、純粋数学の分野を中心に研究を行う傍ら、数学の魅力を伝えるための講演会や中学校・高等学校への出前授業などにも取り組んでいる。著書に『日本一わかりやすいABC予想』(ビジネス教育出版社)、『「数学をする」ってどういうこと?』(技術評論社)など多数。
AIのコントロールには数学が必須。豊かな生活を支える数学の力とは

――はじめに、先生のご専門についてお聞かせください。
自然数や素数をはじめとする整数の性質について研究する整数論が専門です。特に、素数の分布を調べるために考案されたゼータ関数の研究に注力しています。素数にはいまだ多くの謎があり、長きにわたって世界中の数学者を悩ませる「リーマン予想」もその一つ。数学上の重要な未解決問題を内包するゼータ関数は、単なる関数の概念を超越した対象と考えられています。
――応用とは対をなす純粋数学の世界ですね。先生が数学者を志したきっかけは何だったのでしょうか。
小学生の頃、学習帳の表紙裏に書かれた、ドイツの数学者・ガウスのエピソードを目にしました。小学校の教師が「1から100までの数を全部足せ」という問題を出したところ、7歳のガウス少年はわずか数秒でその問題を解いた、という逸話です。1から100までの数を両端から1+100=101、2+99=101、と順に足し合わせていくと101が50組できるから答えは「5050」。これはすごいと、子どもながらに感動したのをきっかけに、数学の面白さに魅了されていきました。
――数学者というと、自身の知的好奇心を満たしながら真理を追究していく姿を思い浮かべますが、現代社会における役割をどのようにお考えですか。
日を追うごとにAIの発達は進み、遠くない未来にシンギュラリティ(技術的特異点)を迎えると言われています。人間の存在が脅かされるのでは、と不安を抱いている人も少なくないと思いますが、そのAIの制御に必要なのが数学です。また、計算や解析はAIの得意分野である一方、数学の価値を理解しそれをもとに思考することができるのは人間だけです。人間とAIが共存する未来を構築していくのが、現代における数学者の役割の一つかもしれません。
――AIを正しく効果的に活用するために、数学が使われるのですね。
数式をAIにインプットして運用すれば、世の中を正しい方向に導くことができます。扶養控除の制度を例にしてみましょう。決められた年収額を超えると扶養から外れ税負担がかかってくるのですが、それが女性の社会進出を阻んでいるという議論があります。数学とAIを活用すれば、グラデーションをつけて控除額を決めることも可能になるはず。より公平な、納得感のある税制を実現できるのではないかと考えています。私たちの生活をより豊かにするために、数学の価値が発揮されてほしいですね。
経済や政治にも寄与する「数学的思考」と、数学が持つ「価値」の正体

――数学の価値とは、具体的にどのようなことを指すのでしょうか。
原点と点(x,y)との距離は
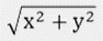 で表される、という三平方の定理を取り上げてみましょう。自宅から最寄りのコンビニまでの距離を知りたいとき、もちろん三平方の定理を使って計算することは可能ですが、実際は地図を見て測った方が早いですよね。数式や定理の価値は、それが実生活に役立つかどうかで決まるものではありません。証明によって得られた本質に着目すると、さらに発展した知を見いだすことができるのが、重要なポイントです。
で表される、という三平方の定理を取り上げてみましょう。自宅から最寄りのコンビニまでの距離を知りたいとき、もちろん三平方の定理を使って計算することは可能ですが、実際は地図を見て測った方が早いですよね。数式や定理の価値は、それが実生活に役立つかどうかで決まるものではありません。証明によって得られた本質に着目すると、さらに発展した知を見いだすことができるのが、重要なポイントです。――三平方の定理の価値は、平面上2点間の距離を導き出せることではないのですか?
たとえば、三平方の定理を3次元空間に拡張したとします。勘の良い方であれば、原点と点P(x,y,z)との距離は、
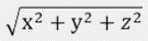 になることが想像できるのではないでしょうか。実は、4次元やそれ以上の次元にも同じ考えを当てはめることが可能です。目に見えない次元においても距離を定義できるようになり、距離という概念の本質が見えたこと、それが三平方の定理の本当の価値だと言えます。
になることが想像できるのではないでしょうか。実は、4次元やそれ以上の次元にも同じ考えを当てはめることが可能です。目に見えない次元においても距離を定義できるようになり、距離という概念の本質が見えたこと、それが三平方の定理の本当の価値だと言えます。――「実生活のこの場面で役に立つ」という個々の事例ではなく、本質的な考え方に真価があるのですね。証明できたからそれで終わり、ではないと。
その通りです。2020年4月、未解決問題であるABC予想(※)を証明したとされる論文が数学専門誌に掲載されましたが、「超難問が解けた」という表層的な部分だけが話題にのぼっていました。ABC予想の性質や、証明できたことによってどのような価値がもたらされるのかといったところが最も重要であるはずが、世間はそこに注目しなかった。「理系分野のことは難しくてよく分からないから、結果だけ教えてくれ」という風潮があるのでしょう。私はそうした世界に危機感を抱いており、教育によって人々の数学的思考を少しでも高めたいと思っています。
――数学的思考ができないと不都合が生じるのでしょうか。
最近だと、新型コロナウイルス感染症の流行初期において、多くの人が「8割の接触機会削減」を「8割の外出削減」と思い込んでいたことがあげられます。接触機会と外出量は比例関係ではなく、接触機会は外出量の2乗に比例するものです。さして複雑ではない計算なのですが、専門家の提唱を反すうせずに飲み込んでしまった方もいるのではないでしょうか。マスコミも8割という数字を大きく取り上げ、「何の8割なのか」をきちんと説明していない報道をしていたように思います。
――確かに「外出はいつもの2割程度に抑えよう」と思って行動していたかもしれません…。私自身も、流れてくる情報をそのまま受け取ってしまう癖がついていたように思います。
社会全体でそのような傾向があると感じますね。先ほどの扶養控除の話に戻ると、「年収が130万円を超えると扶養から外れるので、それ以内に抑えなくては」と深く考えずに既成の制度に従う人が大半でしょう。しかし、1円でもオーバーすると違う制度が適用されるなんて、妙だと思いませんか?そうしたことに疑問を抱いて、今の制度やルールは一体何に基づいて作られたのか自ら考える姿勢が重要だと思っています。きちんと思考できる人が増えると、「数字に境界線はないから税制もグラデーションにしよう」といった主張をする政治家も出てくるかもしれません。
(※)ABC予想…1985年、スイスのデビッド・マッサー氏とフランスのジョゼフ・オステルレ氏により提示された整数論の難問。正の整数aと整数bの「和」であるcと、三つの数a、b、cそれぞれの素因数の「積」を考えた時、和と積の間に、特別な関係があることを示している。
数学は芸術?創造性や思考力を鍛える数字との向き合い方

――数学は経済や政治の世界とも深い関係があり、日常生活において重要な役割を持っていることがよく分かりました。数学的思考を高めたり、数字に強くなったりするにはどうすればいいのでしょうか。
おっしゃるように、身近に数学はあふれています。新型コロナウイルス感染症のワクチン接種率が全人口の50%を超えたとか、ゲームアプリのガチャでレアアイテムが出現する確率は0.001%だとか…。一見どう捉えればいいかよく分からない数字も、注意深く追いかけていくと徐々にその姿が見えてきますよ。「接種率50%と言うけど、身のまわりの若者は接種完了した人が少ないから、高齢者が中心なのかな」「1か月毎日ガチャを引いたら10回当たったから、確率は25~30%くらいかな」と、自分なりのデータを蓄積、分析していくことが大切です。その際にポイントとなるのは、確率に影響を及ぼすファクターの存在も考慮すること。単に2人に1人、30分の10ではなく、「ゆらぎ」があることを理解できると、だいたいこれくらい、という推測が無意識に行えるようになります。
数学的現象を知覚する感覚は「数覚」と呼ばれることがあります。そうした独特の感覚を研ぎ澄ましていって、身のまわりの数字や数式が持つ意味と背景に目を向ける人が増えてほしいと願っています。
――これまで数学は敬遠していましたが、少し興味がわいてきました。先生は数学の魅力をどのようにお考えですか。
社会情勢や政治などに全く影響されない独立した学問であることが、数学の面白いポイントであり、研究のやりがいにもつながっていると感じます。他の学問分野には、時間の流れや世の中の景気や流行に影響を受けやすい研究もあります。しかし、数学の理論や定理は永遠に受け継がれていくもので、一度発見されたら、その価値は1万年後も決して色褪せません。不変性、そして想像を超えた応用性を持つことが数学の魅力だと考えています。
――発見された定理がはるか遠い未来で応用され、その時代の生活を変える可能性もあるのですね。他の分野とはスケールの大きさが違うというか…。
人類の発展や、思考を支えてきたのは数学だと言えるでしょう。永遠に変わらない価値、という点は、音楽や文学といった芸術に通ずる気がします。世に発表された偉大な作品は後世にも語り継がれますし、そこからインスピレーションを受けて新しい芸術が生まれることもありますよね。
――数学者と芸術家は、対極にあるようで意外と近いということですか。
確かにそうかもしれません。芸術家と同じく、数学者には創造性が求められるからです。定理や数式をインプットするだけで満足するのではなく、アレンジや改善はできないか、他のケースに当てはめることはできないかと思案し、自分の力で新しい定理や数式を生み出すのが数学者です。時には数学だけではなく物理学や生物学、ひいては文学や経済学など、異分野の中からアイデアを引っ張ってくることもあるでしょう。先ほど数学は独立した学問と言いましたが、多様な分野の知も欠かせません。あらゆるものを組み合わせて作り上げていく、クリエイティブな考え方や姿勢が重要なのです。
まずは興味のある数字に着目して、その数字は一体なにを表しているのか、どのように導き出されたものなのかを調べてみてください。そして自分で思考し、数字が持つ価値を見いだしてみてください。数学の多様な側面に触れ、面白さ・奥深さを身近に感じてほしいと思います。